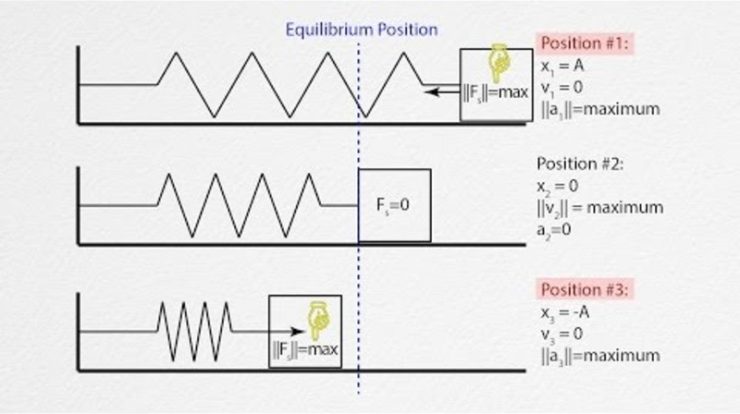
The figure shows a conical pendulum, an apparatus that unveils the captivating world of circular motion and its intricate physical principles. This intriguing device, with its suspended bob tracing a conical path, has captivated scientists and engineers for centuries, inspiring groundbreaking discoveries and practical applications across diverse fields.

The conical pendulum, with its elegant simplicity and profound implications, provides a rich tapestry of physical phenomena to explore. From its mesmerizing oscillations to its mathematical elegance, this apparatus serves as a gateway to understanding the fundamental principles that govern the motion of objects in our universe.

Introduction

A conical pendulum is a pendulum that is suspended from a fixed point and swings in a circular path. The path of the pendulum is a cone, and the period of the pendulum is the time it takes to complete one full cycle.Conical

pendulums have been used for centuries to study the laws of motion. In the 16th century, Galileo Galilei used a conical pendulum to demonstrate that the period of a pendulum is independent of its amplitude. This discovery was a major breakthrough in the development of physics, and it helped to lay the foundation for the modern understanding of motion.

Physical Properties

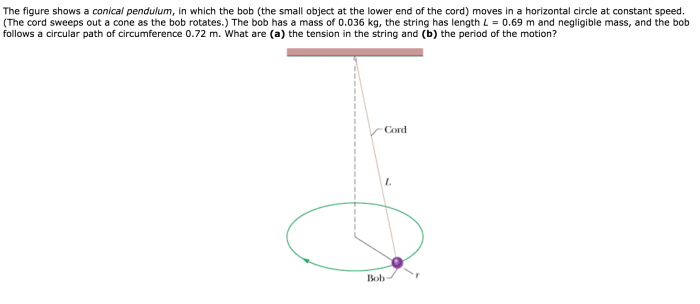
A conical pendulum consists of a small, dense object (the bob) suspended by a string of fixed length. The bob moves in a horizontal circle under the influence of gravity and the tension in the string.

The physical characteristics of a conical pendulum are determined by the following factors:

• Length of the string ( L): The length of the string determines the radius of the circular path of the bob. A longer string results in a larger radius.
• Mass of the bob ( m): The mass of the bob affects the period of oscillation. A heavier bob has a longer period.

Relationship between String Length, Bob Mass, and Period of Oscillation

The period of oscillation ( T) of a conical pendulum is the time it takes for the bob to complete one full circle. The period is related to the length of the string ( L) and the mass of the bob ( m) by the following equation:

T= 2π√( L/ g)

where gis the acceleration due to gravity.

This equation shows that the period of oscillation is directly proportional to the square root of the length of the string and inversely proportional to the square root of the mass of the bob.

Mathematical Analysis

The motion of a conical pendulum can be described by the following equation of motion:

$$ mgl \sin \theta = mv^2 /r $$

where:

• $m$ is the mass of the bob
• $g$ is the acceleration due to gravity
• $l$ is the length of the string
• $\theta$ is the angle between the string and the vertical
• $v$ is the speed of the bob
• $r$ is the radius of the circle in which the bob moves

This equation can be used to derive the angular frequency, amplitude, and phase of the pendulum’s motion.

Angular Frequency

The angular frequency of the pendulum is given by the following equation:

$$ \omega = \sqrtg/l \sin \theta $$

The angular frequency is the rate at which the pendulum rotates around the vertical axis. It is measured in radians per second.

Amplitude

The amplitude of the pendulum’s motion is the maximum angle between the string and the vertical. It is measured in degrees.

Phase

The phase of the pendulum’s motion is the angle between the current position of the bob and the starting position. It is measured in degrees.

Applications

Conical pendulums have a range of practical applications in various fields due to their unique properties and motion characteristics.

In physics, conical pendulums are used to demonstrate and study fundamental principles of mechanics, such as conservation of energy, angular momentum, and centripetal force.

Engineering, The figure shows a conical pendulum

• Vibration analysis:Conical pendulums can be employed as sensitive vibration sensors to detect and measure vibrations in structures, machinery, and other systems.
• Balancing:They are used in balancing machines to detect and correct imbalances in rotating machinery, ensuring smooth operation and reducing vibrations.
• Geophysics:Conical pendulums are used in geophysical surveys to measure the gravitational field of the Earth, providing insights into the Earth’s structure and composition.

Art

• Kinetic sculptures:Conical pendulums are incorporated into kinetic sculptures to create dynamic and visually appealing art installations that explore the interplay of motion, gravity, and balance.
• Choreography:The movement of conical pendulums has inspired choreographers to create dance performances that explore the principles of physics and the aesthetics of motion.

Variations and Extensions

The conical pendulum is a versatile system that has been extended and modified in various ways.

Spherical Pendulum

A spherical pendulum is a generalization of the conical pendulum where the bob moves on the surface of a sphere instead of a circular cone. The equations of motion for a spherical pendulum are more complex than those for a conical pendulum, but the general principles are the same.

Extensions and Modifications

There have been many extensions and modifications to the theory of conical pendulums. Some of these include:

• Damping:The effects of damping on the motion of a conical pendulum can be included in the equations of motion. Damping can cause the pendulum to lose energy and eventually come to rest.
• Driving forces:The pendulum can be driven by an external force, such as a sinusoidal force or a torque. This can cause the pendulum to oscillate with a different frequency than its natural frequency.
• Nonlinear effects:The equations of motion for a conical pendulum can become nonlinear if the amplitude of the oscillations is large. This can lead to a variety of interesting phenomena, such as chaos.

Frequently Asked Questions: The Figure Shows A Conical Pendulum

What is the significance of the conical pendulum?

The conical pendulum is a valuable tool for studying circular motion and its applications. It provides insights into the relationship between the length of the string, the mass of the bob, and the period of oscillation, making it useful in fields such as engineering, physics, and art.

How does the conical pendulum relate to other types of pendulums?

The conical pendulum is a variation of the simple pendulum, but its circular motion introduces additional complexities. It shares similarities with the spherical pendulum, which also exhibits three-dimensional motion, but the conical pendulum’s path is restricted to a cone.

What are some practical applications of the conical pendulum?

The conical pendulum has found applications in various fields. In physics, it is used to demonstrate conservation of energy and angular momentum. In engineering, it is employed in vibration analysis and control systems. Additionally, artists have utilized the pendulum’s motion to create captivating kinetic sculptures.